Keeping Track of Things: Games Architecture
- Sep 18, 2018
- 8 min read
Recently I started doing an unofficial, bi-weekly seminar at NYU's Game Center for the second-year masters students. The second year at NYU is dominated by a thesis project - however, many of the MFA students have never worked on a large-scale project. In fact, many had never programmed before enrolling at NYU. Last year’s thesis projects were all amazing, but some of the students found themselves in the Spring, limited by decisions they’d made earlier in the year - organizational or structural decisions that may have been able to be avoided. So I wanted share a bit of foundational knowledge in software architecture, particularly as relates to game design, and I’ll track those seminars here in this blog.
What Is Games Architecture and Why Do I Care?
Game programming struggles to answer these three concerns - that are always in conflict with each other:
Code should be easy to understand over the lifetime of the project.
The game needs to run fast.
Developers need iterate and make huge changes quickly.
Games architecture (like any kind of software architecture) deals with fundamental structural choices around a project – the things that are difficult or costly to change. If you design an SHMUP with a dozen different classes for types of enemies, each with their own internal logic and decision trees, at a certain point it becomes very difficult to decide you want them to all inherit from a single class, or to track and make large decisions about all the enemies at once.
Good architecture decreases the cognitive load of iterating, making changes quickly, fixing bugs, and adding features. In my opinion, it does this by:
Simplifying the Mental Model: Good architecture makes your code more closely match the actual features of your game. The Behavior Tree is a great example of this - you take a bunch of complicated nested if statements that are difficult to read, and turn it into a series of prioritized decisions the AI is making. You don’t need to remember the mindset you were in when you designed it to make changes - you just have to decide what the AI can do, and prioritize that list (or tree) of things.
Decoupling Your Code: Your code becomes more organized the more you use good architecture, and the ways it communicates become more streamlined. Suddenly, the gun in your game doesn’t know how to make a laser beam in order to shoot - it just “shoots”. The closer your code becomes to a group of objects acting the way you expect them to act, the easier it is for the whole team to make positive contributions to the project.
Speeding Up Iteration: When you make good software architecture, you plan not just for the current version of the game, but what the game could be. By abstracting the logic of your software, and organizing it, it becomes easier and easier to make new and faster choices and implement them.
Most of this writing will focus on the Unity3D engine, as that’s what’s primarily used at NYU’s Game Center - but the ideas expressed will work in any game engine, or in no engine at all. In fact, the architecture patterns I’ll be discussing are general enough to apply to almost any kind of programming - although the explanations and focus in this writing will be on games.
And before I go on, I wanted to explain what a pattern is - in software design, there are kinds of problems that come up over and over again. Whenever you come upon a tough problem, there’s a really good chance that some other programmer had wrestled with a similar problem, found a clever solution, and then abstracted it. If enough people thought that was a good solution, well - that becomes a programming pattern. The thing to remember is that you don’t need to use a pattern just because you know it, and you will never need to know every single programming pattern. It’s really easy to fall into the trap of over-engineering your projects (I find myself doing this all the time), and usually when you’re prototyping, it’s better to make messy code quickly, than make an entire system that you find you won’t actually need. Just remember to go back and clean it up before it’s too late!
Oh, and one last thing - my foundation in this comes primarily from my computer science background, but I would have been lost when I made the switch to game design without Gameplay Programming Patterns, an unbelievable website to which I will be referring to often, as it provides a lot of the games-specific foundational knowledge I will be using. And personally, I would know far less on these topics without Mattia Romeo of Gigantic Mechanic, who has given selflessly of his personal time to help make me a better programmer and designer.
How to Track “Things”
Each of these seminars, I decided to tackle a larger, bigger problem that tends to come up in Game Design, and for the first one, I decided to start with finding and keeping track of things. When a new programmer first starts out in an engine like Unity, it’s very common to simply use the built in “find” functionality, usually one that searches for specific entities or objects by an index, tag, or even worse, a string literal.
Why is it bad to search for something by its ‘name’? This is where decreasing the amount of things you have to remember comes into play. If you decide to find your GameController every time you need it by searching for an object called “GameController” that it’s attached to, well - what about three months from now, when you decide to call that object “Game Manager”? Or when you start having multiple levels or locations, each with their own manager? You either have to start putting together code to change the string you’re searching for in different scenarios, and remember to change the string you’re searching for every time you make a change. Plus, referring to anything by a string is tricky. It may seem the same as using a variable name, but your compiler won’t double check that there’s something with that string in your game before compiling, and won’t know how to warn you. This is the same reason I tend to advise against using UnityEngine.Find(“Name of Object”), and UnityEngine.Invoke(“Name of Function”). They’re both dangerous for similar reasons - if you change the name of the thing it’s referring to, you’ll have bugs and errors that may be difficult to find.
As people move on in their programming experience, usually the next thing they learn is the Singleton Pattern, usually without realizing it’s a pattern. Somewhere on the internet, they see this piece of code:

And they have the ability to find their GameController anywhere! This seems almost magical when it’s first discovered, but there are some issues with this, particularly in the context of games.
Why is the singleton pattern so bad? This one’s pretty easy - it isn’t! Except when it is. Clear? Well - a singleton is really useful because of two things - accessibility, and uniqueness. When you create a singleton, you’re saying “there is one, and only one, instance of this class of objects that will matter, so if you’re talking about an object of this type, well, there’s only one that matters, so we’ll make it really easy to find.” Most of the time, when people use the singleton pattern, they need the accessibility, but don’t actually need the uniqueness. This becomes a problem, particularly in games programming, where we often have multiple levels, or states, or conditions that change the services we’re using (like the LevelManager may be specific to a certain level, or we need a different EnemyManager for the boss level).
Plus, well - singletons increase coupling, which makes it much harder to reason about code. You have to consider all of your singleton’s code whenever there’s a bug in anything that references it. And, for those of you with more programming and complexity background, they aren’t concurrency friendly. Having a big chunk of memory that everything can access means your multiple threads or cores start having synchronization-related bugs (deadlocks, race conditions, etc.).
An Answer? The Service Locator
Here comes a pattern to save the day! The Service Locator acts like a kind of “phone book” for the core systems in your game - instead of a unique, single place that holds a static reference to an instance of a class, you have a decoupled, specific list of what things you need references to in your game. Often it will look essentially like this (although there are more complicated setups possible) -
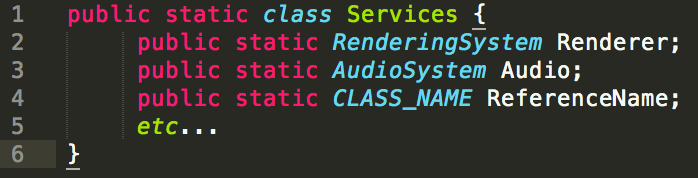
You might be asking, “What does this get me?” Well, here’s a list:
Access: In all the rest of your code, you can say “Services.Renderer” and immediately be able to make use of an instance of the renderer. Instead of needing to find an object, or have a singleton of an object, you have a “phone book”, a place to find that specific object you need.
Hot-Swapping: You can change the actual instance it’s referring to whenever you want, and have direct control of the order these objects are initialized and changed. Say you need a different LevelManager for each level. Initialize a new one every time you switch levels, and you’re set - you don’t have to update anything else about what level you’re on. Have a different RenderingSystem depending on the target platform? Perfect - you can swap out the rendering system depending on the build without having to make multiple versions of your game.
Testing: It may be really inconvenient to load a full version of your game every time you want to test a system - you can make dummy versions of every system you’re not testing and just work on the specific system you’re testing.
Multiplicity: If you have a system you need multiple versions of - a common example is to need multiple player controllers for a multiplayer game. Well, you can keep multiple references to a single class (something difficult with singletons), and choose the order you instantiate them, and with what settings. This is unbelievably useful as your code gets more complicated, and you want to adjust configuration and settings depending on who’s in the game, and who has entered in what order.
Another Answer? The Manager Pattern
This one I think is less of an established pattern is the “manager pattern”. The reason in traditional software architecture that people are pretty against the idea of having a “manager class”, for reasons that are valuable in non-games software architecture (it’s a kind of mushy delineation of concerns, it’s not very complete, etc., etc.), but there are all kinds of reasons in game design where having a layer of abstraction over a collection of entities makes a lot of sense - we often need to, from a design perspective, consider our game as different collections of things we’re manipulating - enemies, items, players, etc. And as a bonus, it lowers the complexity of managing them, and decreases coupling by hiding the implementation details of those instances of a group of objects.
In gameplay programming (and this is very influenced by Mattia Romeo), I think it’s very useful to have a manager or system that models a group or collective property, and allows easy access for:
Lifecycle Control: How and when things in that group are created, updated, and destroyed.
Access: Simplify tracking and control of individuals within that group, and provide an interface.
Queries: Allow queries across the managed instances
For this, however, it’s far more difficult to provide a simple and straightforward example - it’s more a pattern of thinking than a clear-cut programming pattern. As an example, I’ve made this Unity3D project that shows both of these patterns in a clear-cut, simple way.







Comments